字数

365 字

阅读时间

2 分钟

Eigen vector and value

几何意义

经过线性变换后，仍保留在原本直线上的向量，称为特征向量。其缩放比例称为特征值。

用下面的公式解释：对一个向量进行线性变换，结果等于对该向量进行数乘

$$A\overrightarrow{v}=\lambda \overrightarrow{v}$$

求解特征值：

$$(A-\lambda I)\overrightarrow{v}=\overrightarrow{0}$$

如果要求解非零特征向量，就需要令 $det(A-\lambda I)=0$ 用几何的视角去解释就是将向量 $\overrightarrow{v}$ 压缩一个维度。参考平面压缩，行列式为0

梳理一下就是：$(A-\lambda I)$ 将 $\overrightarrow{v}$ 压缩为零向量 $\stackrel{\mathrm{等}\mathrm{价}\mathrm{于}}{⟷}$ A 对 $\overrightarrow{v}$ 线性变换后只是长度上的伸缩

当计算的特征值中出现复数时，一般对应于变换中的某种旋转。

特征基

对于对角矩阵（Diagonal matrix）：所有的基向量都是特征向量。 对于对角矩阵，很容易计算高次方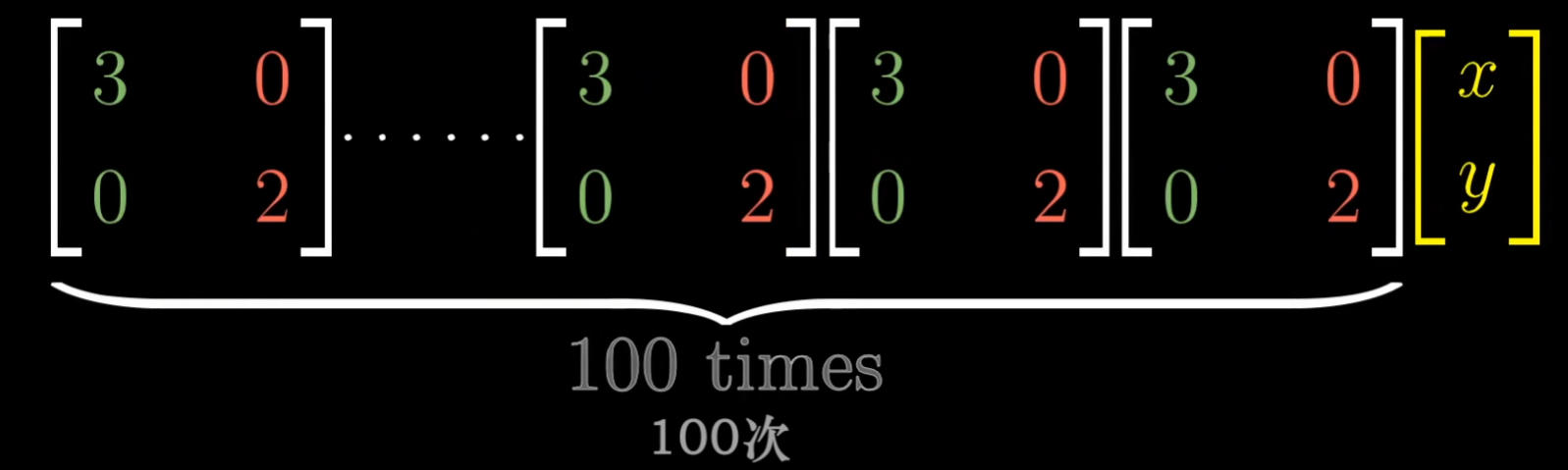： 而对于非对角矩阵，就有点困难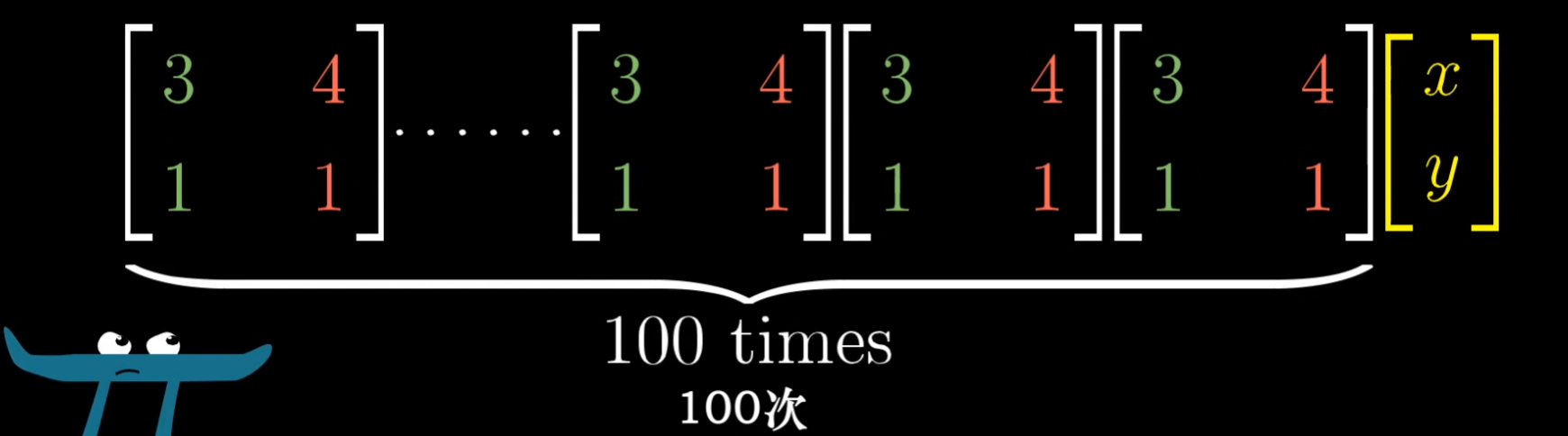： 当你的特征向量足够多，可以选出作为张成整个空间的基向量。那么你就可以变换坐标系，使特征向量就是基向量。 1. 向量到底是什么？ 涉及到 6. 基变换的知识。

贡献者

OveDuke

文件历史

最后编辑于 2 天前查看完整历史

6dee2-update_finalImage

83fe4-img_00

86b92-image

b708d-update_imagename